1. 雅可比矩阵:"Jacobian"矩阵
在向量微积分中,雅可比矩阵是一阶偏导数以一定方式排列成的矩阵,雅可比矩阵类似于多元函数的导数,其行列式称为雅可比行列式;雅可比矩阵的重要性在于体现了一个可微方程与给定点的最优线性逼近,可进行非线性方程组在参考点的线性化,类如无人驾驶控制中线性模型预测控制需要的线性对象。
定义:假设是一个从n维欧氏空间映射到到m维欧氏空间的函数。这个函数由m个实函数组成![]() 这些函数的偏导数(如果存在)可以组成一个m行n列的矩阵,这个矩阵就是所谓的雅可比矩阵:
这些函数的偏导数(如果存在)可以组成一个m行n列的矩阵,这个矩阵就是所谓的雅可比矩阵:
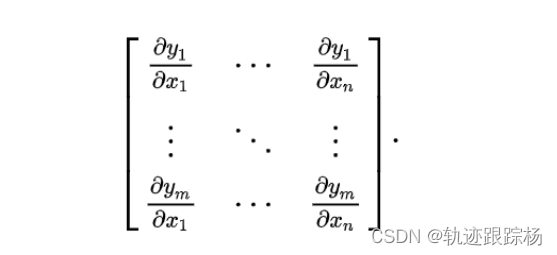
此矩阵用符号表示为:
由于矩阵描述了向量空间中的运动——变换,而雅可比矩阵看作是将点转化到点,或者说是从一个n维的欧式空间转换到m维的欧氏空间。如果m=n,可以定义雅可比矩阵的行列式,也就是雅可比行列式(Jacobian determinant)。
如果p是函数组中的一点,F在p点可微分,根据高等微积分,是在这点的导数。在此情况下,这个线性映射即F在点p附近的最优线性逼近,也就是说当x足够靠近点p时,我们有:
![]()
2. 雅可比行列式
雅可比行列式通常称为雅可比式(Jacobian),它是以n个n元函数的偏导数为元素的行列式 。事实上,在函数都连续可微(即偏导数都连续)的前提之下,它就是函数组的微分形式下的系数矩阵(即雅可比矩阵)的行列式。雅可比行列式是以n个n元函数 的偏导数为元素的行列式,常记为:
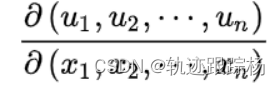
事实上,在函数都连续可微(即偏导数都连续)的前提之下,函数组的微分形式为:
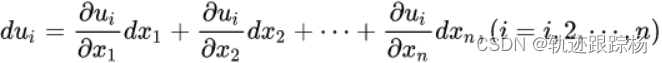
雅可比行列式是上述微分形式的系数矩阵(即雅可比矩阵)的行列式。
具体例子:(车辆动力学模型线性化)
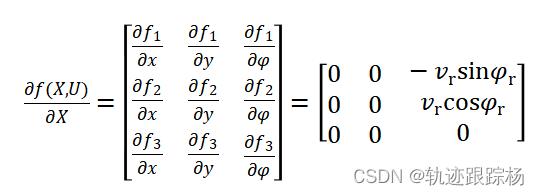
来源知乎学习:雅可比矩阵和雅可比行列式 - 知乎




