DTW 简介

DTW 定义

动态时间规整（Dynamic Time Warping，DTW）用于比较具有不同长度的两个阵列或时间序列之间的相似性或距离。

假设要计算两个等长数组的距离：

a = [1, 2, 3]
b = [3, 2, 2]

最简单的使用欧氏距离进行计算，但如果 a 和 b 的长度不同怎么办？

a = [1, 2, 3]
b = [2, 2, 2, 3, 4]

DTW 解决了这个问题，正如其名，规整序列以使其匹配。比较不同长度的数组的想法是建立一对多和多对一的匹配，这样两者之间的总距离可以最小化。

假设我们有两个不同的数组，红色和蓝色，不同的长度：

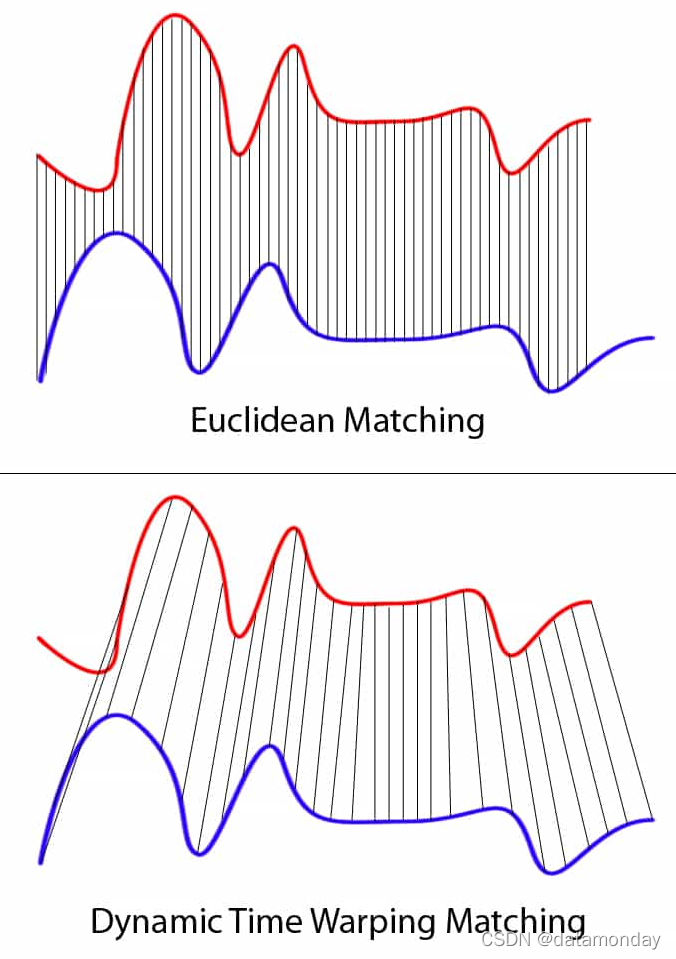
显然这两个序列遵循相同的模式，但蓝色曲线比红色曲线长。如果我们应用顶部所示的一对一匹配，则映射不会完全同步，蓝色曲线的尾部会被遗漏。DTW 通过开发一对一解决了这个问题许多匹配使得具有相同模式的波谷和波峰完美匹配，并且两条曲线都没有遗漏（图片底部）。

DTW 计算过程

DTW 是一种计算两个给定序列（例如时间序列）之间的最佳匹配的方法：

• 第一个序列中的每个索引必须与另一个序列中的一个或多个索引匹配，反之亦然
• 第一个序列的第一个索引必须与另一个序列的第一个索引匹配（但它不必是唯一匹配）
• 第一个序列的最后一个索引必须与另一个序列的最后一个索引匹配（但不一定是唯一匹配）
• 第一个序列的索引到另一个序列的索引的映射必须是单调递增的，并且反之亦然，即如果 j > i 是来自第一个序列的索引，则在另一个序列中不能有两个索引 l > k，这样索引 i 与索引 l 匹配，索引 j 与索引 k 匹配，反之亦然

最佳匹配由满足所有其余部分的匹配表示 rictions 和 rules 并且具有最小代价，其中代价计算为每个匹配的索引对在它们的值之间的绝对差的总和。

总而言之，head 和 tail 必须在位置上匹配，没有交叉匹配，也没有被遗漏。

DTW 形式化定义

动态时间规整（DTW）可以在一定的限制下找到两个给定（时间相关）序列之间的最佳对齐（图 4.1）。直观地说，序列以非线性方式规整以相互匹配。最初，DTW 已被用于比较自动语音识别中的不同语音模式，参见 [170]。在数据挖掘和信息检索等领域，DTW 已成功应用于自动处理与时间相关时变和不同速度的数据。

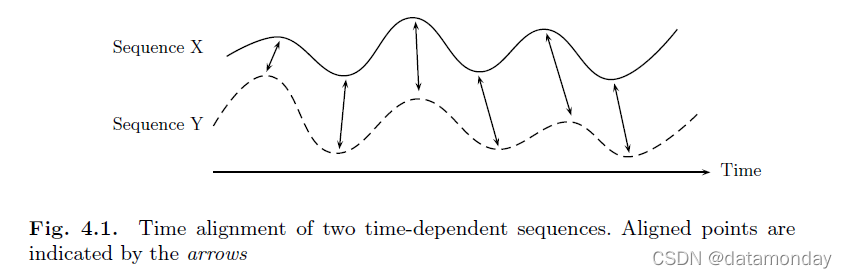
经典的 DTW

DTW 的目标是比较长度为 $N\in \mathbb{N}$ 的两个（时间相关）序列 X : = ( x 1 , x 2 , . . . , x N ) X := (x_1, x_2, ..., x_N) X:=(x1​,x2​,...,xN​) 和长度为 Y : = ( y 1 , y 2 , . . . , y M )   M ∈ N Y := (y_1, y_2, ..., y_M) M ∈ N Y:=(y1​,y2​,...,yM​) M∈N。这些序列可能是离散信号（时间序列），更一般地说，是在等距时间点采样的特征序列。在下文中，我们固定一个由 $\mathcal{F}$ 表示的特征空间。对于 $n\in [1:N]$ 和 $m\in [1:M]$， x n , y m ∈ F x_n, y_m in mathcal{F} xn​,ym​∈F 。为了比较两个不同的特征 $x,y\in \mathcal{F}$，需要一个局部代价度量，有时也称为局部距离度量，它被定义为一个函数

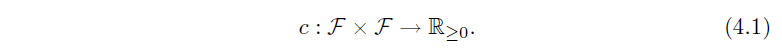
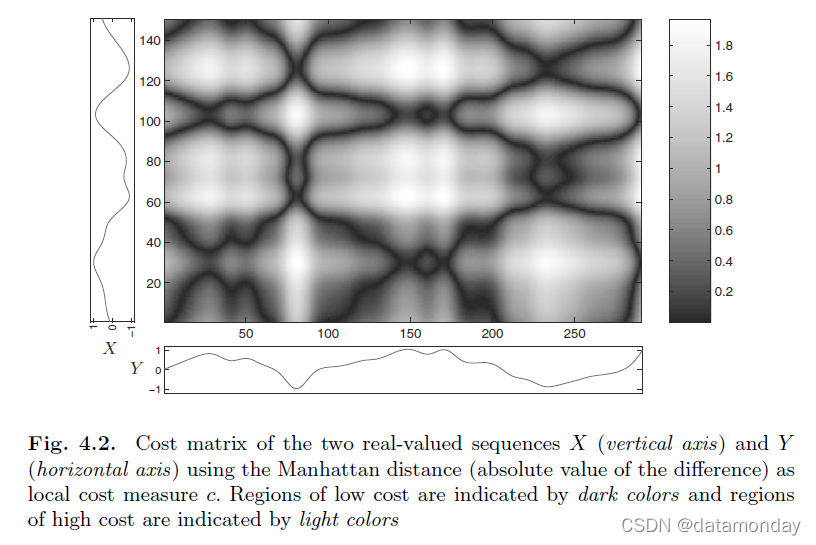
通常，如果 $x$ 和 $y$ 彼此相似，则 $c(x,y)$ 小（代价低），否则 $c(x,y)$ 大（代价高）。评估序列 $X$ 和 $Y$ 的每一对元素的局部代价度量，得到由 C ( n , m ) : = c ( x n , y m ) C(n, m) : = c(x_n, y_m) C(n,m):=c(xn​,ym​) 定义的代价矩阵 C ∈ R N × M C ∈ R^{N×M} C∈RN×M，见图 4.2。然后目标是在 $X$ 和 $Y$ 之间找到一个总体代价最小的对齐方式。直观地说，这样的最佳对齐沿着代价矩阵 $C$ 内的低代价“谷”运行，参见图 4.4 的说明。下一个定义形式化了对齐的概念。


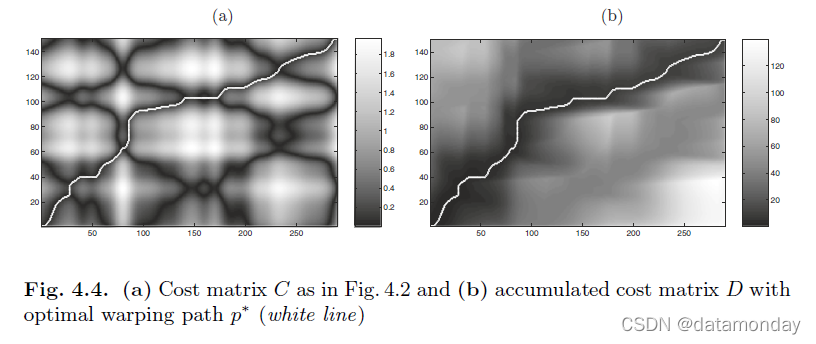
注意，步长条件 (iii) 意味着单调性条件 (ii)。$(N,M)$-warping path p = ( p 1 , . . . , p L ) p = (p_1, ..., p_L) p=(p1​,...,pL​) 定义了两个序列 X = ( x 1 , x 2 , . . . , x N ) X = (x_1, x_2, ..., x_N ) X=(x1​,x2​,...,xN​) 和 Y = ( y 1 , y 2 , . . . , y M ) Y = (y_1, y_2, ... , y_M) Y=(y1​,y2​,...,yM​) 之间的对齐，通过将 $X$ 的元素 x n l x_{n_l} xnl​​ 分配给 $Y$ 的元素 y m l y_{m_l} yml​​ 。

• 边界条件强制 $X$ 和 $Y$ 的第一个元素以及 $X$ 和 $Y$ 的最后一个元素相互对齐。换句话说，对齐（alignment）是指整个序列 $X$ 和 $Y$。
• 单调性条件反映了忠实计时（faithful timing）的要求：如果 $X$ 中的一个元素先于第二个元素，这也应该适用于 $Y$ 中的相应元素，反之亦然。
• 步长条件表达了一种连续性条件：$X$ 和 $Y$ 中的任何元素都不能省略，并且对齐中没有重复，即规整路径 $p$ 中包含的所有索引对都是成对不同的。

图 4.3 说明了这三个条件。如果理解了上边提到的三个条件，这三幅图也很好明白。图 b 违反了边界条件，即第一个元素和最后一元素都没有分别对齐。图 c 违反了单调性，即序列 Y 的时刻超过了 X 的时刻（横轴的 3,4），因为 Y 是短的序列，它的元素索引不能大于较长的序列 X 否则会导致重复映射的情况，因为后边的元素不够分了，这在图 c 中也可以很清晰的看出来。图 d 违反了连续性条件，即两个序列之间的对齐不能跳过元素。

$X$ 和 $Y$ 之间相对于局部代价度量 $c$ 的总代价 c p ( X , Y ) c_p(X, Y ) cp​(X,Y) 定义为

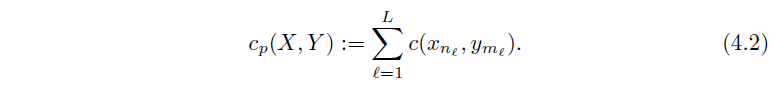
此外，$X$ 和 $Y$ 之间的最佳规整路径（wraping path）是在所有可能的规整路径中总代价最小的规整路径 p ∗ p^* p∗。然后将 $X$ 和 $Y$ 之间的 DTW 距离 $DTW(X,Y)$ 定义为 p ∗ p^* p∗ 的总代价：

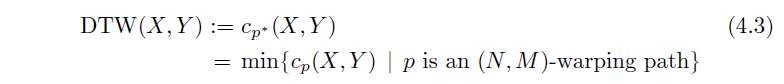
我们继续对 DTW 距离进行一些评论。

• 首先，请注意 DTW 距离是明确定义的，即使可能存在若干条总代价最低的规整路径（wrapping path）。
• 其次，在局部代价度量 $c$ 对称的情况下，很容易看出 DTW 距离是对称的。然而，即使 $c$ 成立，DTW 距离通常也不是正定的。例如，在 c ( x 1 ， x 1 ) = c ( x 2 ， x 2 ) = 0 c(x_1，x_1) = c(x_2，x_2) = 0 c(x1​，x1​)=c(x2​，x2​)=0 的情况下，对于序列 X : = ( x 1 ， x 2 ) X := (x_1，x_2) X:=(x1​，x2​) 和 Y : = ( x 1 ， x 1 ， x 2 ， x 2 ) Y := (x_1，x_1，x_2，x_2) Y:=(x1​